L'algorithme de Bellman Ford est un algorithme de chemin le plus court à source unique. Cet algorithme est utilisé pour trouver la distance la plus courte entre un sommet unique et tous les autres sommets d'un graphe pondéré. Il existe divers autres algorithmes utilisés pour trouver le chemin le plus court, comme l'algorithme de Dijkstra, etc. Si le graphique pondéré contient des valeurs de poids négatives, l'algorithme de Dijkstra ne confirme pas s'il produit la bonne réponse ou non. Contrairement à l'algorithme de Dijkstra, l'algorithme de Bellman Ford garantit la bonne réponse même si le graphique pondéré contient des valeurs de poids négatives.
Règle de cet algorithme
We will go on relaxing all the edges (n - 1) times where, n = number of vertices
Considérez le graphique ci-dessous :
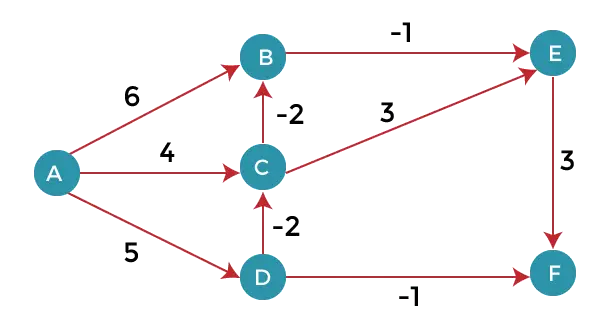
Comme nous pouvons le constater dans le graphique ci-dessus, certains poids sont négatifs. Le graphique ci-dessus contient 6 sommets, nous allons donc continuer à nous détendre jusqu'aux 5 sommets. Ici, on va détendre tous les bords 5 fois. La boucle répétera 5 fois pour obtenir la bonne réponse. Si la boucle est itérée plus de 5 fois, la réponse sera également la même, c'est-à-dire qu'il n'y aura aucun changement dans la distance entre les sommets.
Se détendre signifie :
où se trouve la touche Insérer sur le clavier d'un ordinateur portable
If (d(u) + c(u , v) <d(v)) d(v)="d(u)" + c(u , v) < pre> <p>To find the shortest path of the above graph, the first step is note down all the edges which are given below:</p> <p>(A, B), (A, C), (A, D), (B, E), (C, E), (D, C), (D, F), (E, F), (C, B)</p> <p>Let's consider the source vertex as 'A'; therefore, the distance value at vertex A is 0 and the distance value at all the other vertices as infinity shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-2.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph has six vertices so it will have five iterations.</p> <p> <strong>First iteration</strong> </p> <p>Consider the edge (A, B). Denote vertex 'A' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 6</p> <p>Since (0 + 6) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 6 = 6</p> <p>Therefore, the distance of vertex B is 6.</p> <p>Consider the edge (A, C). Denote vertex 'A' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex C is 4.</p> <p>Consider the edge (A, D). Denote vertex 'A' as 'u' and vertex 'D' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex D is 5.</p> <p>Consider the edge (B, E). Denote vertex 'B' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 6</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (6 - 1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 6 - 1= 5</p> <p>Therefore, the distance of vertex E is 5.</p> <p>Consider the edge (C, E). Denote vertex 'C' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 4</p> <p>d(v) = 5</p> <p>c(u , v) = 3</p> <p>Since (4 + 3) is greater than 5, so there will be no updation. The value at vertex E is 5.</p> <p>Consider the edge (D, C). Denote vertex 'D' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = -2</p> <p>Since (5 -2) is less than 4, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 2 = 3</p> <p>Therefore, the distance of vertex C is 3.</p> <p>Consider the edge (D, F). Denote vertex 'D' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (5 -1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 1 = 4</p> <p>Therefore, the distance of vertex F is 4.</p> <p>Consider the edge (E, F). Denote vertex 'E' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = 3</p> <p>Since (5 + 3) is greater than 4, so there would be no updation on the distance value of vertex F.</p> <p>Consider the edge (C, B). Denote vertex 'C' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 3</p> <p>d(v) = 6</p> <p>c(u , v) = -2</p> <p>Since (3 - 2) is less than 6, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 3 - 2 = 1</p> <p>Therefore, the distance of vertex B is 1.</p> <p>Now the first iteration is completed. We move to the second iteration.</p> <p> <strong>Second iteration:</strong> </p> <p>In the second iteration, we again check all the edges. The first edge is (A, B). Since (0 + 6) is greater than 1 so there would be no updation in the vertex B.</p> <p>The next edge is (A, C). Since (0 + 4) is greater than 3 so there would be no updation in the vertex C.</p> <p>The next edge is (A, D). Since (0 + 5) equals to 5 so there would be no updation in the vertex D.</p> <p>The next edge is (B, E). Since (1 - 1) equals to 0 which is less than 5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(E) = d(B) +c(B , E)</p> <p>= 1 - 1 = 0</p> <p>The next edge is (C, E). Since (3 + 3) equals to 6 which is greater than 5 so there would be no updation in the vertex E.</p> <p>The next edge is (D, C). Since (5 - 2) equals to 3 so there would be no updation in the vertex C.</p> <p>The next edge is (D, F). Since (5 - 1) equals to 4 so there would be no updation in the vertex F.</p> <p>The next edge is (E, F). Since (5 + 3) equals to 8 which is greater than 4 so there would be no updation in the vertex F.</p> <p>The next edge is (C, B). Since (3 - 2) equals to 1` so there would be no updation in the vertex B.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-3.webp" alt="Bellman-Ford Algorithm"> <p> <strong>Third iteration</strong> </p> <p>We will perform the same steps as we did in the previous iterations. We will observe that there will be no updation in the distance of vertices.</p> <pre> The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3 </pre> <p> <strong>Time Complexity</strong> </p> <p>The time complexity of Bellman ford algorithm would be O(E|V| - 1).</p> <pre> function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></-></pre></d(v))>
d(v) = 0 + 6 = 6
La distance du sommet B est donc 6.
Considérons le bord (A, C). Désignons le sommet « A » par « u » et le sommet « C » par « v ». Utilisez maintenant la formule relaxante :
d(u) = 0
d(v) = ∞
c(u, v) = 4
Puisque (0 + 4) est inférieur à ∞, alors mettez à jour
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
La distance du sommet C est donc 4.
Considérons le bord (A, D). Désignons le sommet « A » par « u » et le sommet « D » par « v ». Utilisez maintenant la formule relaxante :
d(u) = 0
d(v) = ∞
c(u, v) = 5
Puisque (0 + 5) est inférieur à ∞, alors mettez à jour
d(v) = d(u) + c(u , v)
d(v) = 0 + 5 = 5
La distance du sommet D est donc 5.
Considérons le bord (B, E). Désignons le sommet « B » par « u » et le sommet « E » par « v ». Utilisez maintenant la formule relaxante :
d(u) = 6
d(v) = ∞
c(u, v) = -1
Puisque (6 - 1) est inférieur à ∞, alors mettez à jour
d(v) = d(u) + c(u , v)
d(v) = 6 - 1= 5
La distance du sommet E est donc 5.
Considérons le bord (C, E). Désignons le sommet « C » par « u » et le sommet « E » par « v ». Utilisez maintenant la formule relaxante :
d(u) = 4
d(v) = 5
c(u, v) = 3
Puisque (4 + 3) est supérieur à 5, il n’y aura donc pas de mise à jour. La valeur au sommet E est 5.
Considérons le bord (D, C). Désignons le sommet «D» par «u» et le sommet «C» par «v». Utilisez maintenant la formule relaxante :
d(u) = 5
d(v) = 4
c(u, v) = -2
Puisque (5 -2) est inférieur à 4, alors mettez à jour
d(v) = d(u) + c(u , v)
d(v) = 5 - 2 = 3
La distance du sommet C est donc 3.
Considérons le bord (D, F). Désignons le sommet «D» par «u» et le sommet «F» par «v». Utilisez maintenant la formule relaxante :
d(u) = 5
d(v) = ∞
c(u, v) = -1
Puisque (5 -1) est inférieur à ∞, alors mettez à jour
d(v) = d(u) + c(u , v)
d(v) = 5 - 1 = 4
La distance du sommet F est donc 4.
les meilleures voitures du monde
Considérons le bord (E, F). Désignons le sommet « E » par « u » et le sommet « F » par « v ». Utilisez maintenant la formule relaxante :
d(u) = 5
d(v) = ∞
c(u, v) = 3
Puisque (5 + 3) est supérieur à 4, il n'y aurait donc aucune mise à jour de la valeur de distance du sommet F.
Considérons le bord (C, B). Désignons le sommet «C» par «u» et le sommet «B» par «v». Utilisez maintenant la formule relaxante :
d(u) = 3
d(v) = 6
c(u, v) = -2
Puisque (3 - 2) est inférieur à 6, alors mettez à jour
d(v) = d(u) + c(u , v)
d(v) = 3 - 2 = 1
La distance du sommet B est donc 1.
La première itération est désormais terminée. Nous passons à la deuxième itération.
Deuxième itération :
Lors de la deuxième itération, nous vérifions à nouveau toutes les arêtes. La première arête est (A, B). Puisque (0 + 6) est supérieur à 1, il n'y aurait donc pas de mise à jour dans le sommet B.
L'arête suivante est (A, C). Puisque (0 + 4) est supérieur à 3, il n'y aurait donc pas de mise à jour dans le sommet C.
L'arête suivante est (A, D). Puisque (0 + 5) est égal à 5, il n'y aurait donc pas de mise à jour au sommet D.
L'arête suivante est (B, E). Puisque (1 - 1) est égal à 0, ce qui est inférieur à 5, mettez à jour :
d(v) = d(u) + c(u, v)
d(E) = d(B) +c(B , E)
= 1 - 1 = 0
L'arête suivante est (C, E). Puisque (3 + 3) est égal à 6 qui est supérieur à 5 il n'y aurait donc pas de mise à jour au sommet E.
L'arête suivante est (D, C). Puisque (5 - 2) est égal à 3, il n'y aurait donc pas de mise à jour au sommet C.
L'arête suivante est (D, F). Puisque (5 - 1) est égal à 4, il n'y aurait donc pas de mise à jour au sommet F.
L'arête suivante est (E, F). Puisque (5 + 3) est égal à 8 qui est supérieur à 4 donc il n'y aurait pas de mise à jour dans le sommet F.
L'arête suivante est (C, B). Puisque (3 - 2) est égal à 1, il n'y aurait donc pas de mise à jour dans le sommet B.

Troisième itération
Nous effectuerons les mêmes étapes que lors des itérations précédentes. Nous observerons qu'il n'y aura pas de mise à jour de la distance des sommets.
The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3
Complexité temporelle
La complexité temporelle de l'algorithme de Bellman Ford serait O(E|V| - 1).
function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></->
d(v) = 0 + 5 = 5
La distance du sommet 3 est donc 5.
Considérons le bord (1, 2). Désignons le sommet « 1 » par « u » et le sommet « 2 » par « v ». Utilisez maintenant la formule relaxante :
d(u) = 0
d(v) = ∞
c(u, v) = 4
Puisque (0 + 4) est inférieur à ∞, alors mettez à jour
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
La distance du sommet 2 est donc 4.
Considérez le bord (3, 2). Désignons le sommet « 3 » par « u » et le sommet « 2 » par « v ». Utilisez maintenant la formule relaxante :
d(u) = 5
d(v) = 4
c(u, v) = 7
méthodes de chaîne en Java
Puisque (5 + 7) est supérieur à 4, il n'y aurait donc pas de mise à jour dans le sommet 2.
Considérez le bord (2, 4). Désignons le sommet « 2 » par « u » et le sommet « 4 » par « v ». Utilisez maintenant la formule relaxante :
d(u) = 4
d(v) = ∞
c(u, v) = 7
Puisque (4 + 7) est égal à 11, ce qui est inférieur à ∞, mettez donc à jour
d(v) = d(u) + c(u , v)
d(v) = 4 + 7 = 11
La distance du sommet 4 est donc 11.
Considérez le bord (4, 3). Désignons le sommet « 4 » par « u » et le sommet « 3 » par « v ». Utilisez maintenant la formule relaxante :
d(u) = 11
d(v) = 5
c(u, v) = -15
Puisque (11 - 15) est égal à -4, ce qui est inférieur à 5, mettez donc à jour
d(v) = d(u) + c(u , v)
d(v) = 11 - 15 = -4
Par conséquent, la distance du sommet 3 est de -4.
Passons maintenant à la deuxième itération.
Deuxième itération
Maintenant, encore une fois, nous allons vérifier tous les bords. La première arête est (1, 3). Puisque (0 + 5) est égal à 5 qui est supérieur à -4 il n'y aurait donc pas de mise à jour dans le sommet 3.
L'arête suivante est (1, 2). Puisque (0 + 4) est égal à 4, il n'y aurait donc pas de mise à jour au sommet 2.
L'arête suivante est (3, 2). Puisque (-4 + 7) est égal à 3, ce qui est inférieur à 4, mettez à jour :
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -4 + 7 = 3
Par conséquent, la valeur au sommet 2 est 3.
L'arête suivante est (2, 4). Puisque ( 3+7) est égal à 10, ce qui est inférieur à 11, mettez à jour
d(v) = d(u) + c(u, v)
d(4) = d(2) +c(2, 4)
= 3 + 7 = 10
Par conséquent, la valeur au sommet 4 est 10.
table de hachage java
L'arête suivante est (4, 3). Puisque (10 - 15) est égal à -5, ce qui est inférieur à -4, mettez à jour :
d(v) = d(u) + c(u, v)
d(3) = d(4) +c(4, 3)
= 10 - 15 = -5
Par conséquent, la valeur au sommet 3 est -5.
Passons maintenant à la troisième itération.
Troisième itération
Maintenant encore, nous allons vérifier tous les bords. La première arête est (1, 3). Puisque (0 + 5) est égal à 5 qui est supérieur à -5 il n'y aurait donc pas de mise à jour dans le sommet 3.
L'arête suivante est (1, 2). Puisque (0 + 4) est égal à 4 qui est supérieur à 3 il n'y aurait donc pas de mise à jour dans le sommet 2.
L'arête suivante est (3, 2). Puisque (-5 + 7) est égal à 2, ce qui est inférieur à 3, mettez à jour :
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -5 + 7 = 2
Par conséquent, la valeur au sommet 2 est 2.
L'arête suivante est (2, 4). Puisque (2 + 7) est égal à 9, ce qui est inférieur à 10, mettez à jour :
d(v) = d(u) + c(u, v)
d(4) = d(2) +c(2, 4)
= 2 + 7 = 9
Par conséquent, la valeur au sommet 4 est 9.
L'arête suivante est (4, 3). Puisque (9 - 15) est égal à -6, ce qui est inférieur à -5, mettez à jour :
d(v) = d(u) + c(u, v)
d(3) = d(4) +c(4, 3)
= 9 - 15 = -6
Par conséquent, la valeur au sommet 3 est -6.

Puisque le graphe contient 4 sommets, donc selon l'algorithme de Bellman Ford, il n'y aurait que 3 itérations. Si nous essayons d'effectuer 4èmeitération sur le graphique, la distance entre les sommets et le sommet donné ne doit pas changer. Si la distance varie, cela signifie que l’algorithme de Bellman Ford ne fournit pas la bonne réponse.
4èmeitération
La première arête est (1, 3). Puisque (0 +5) est égal à 5, ce qui est supérieur à -6, il n'y aurait donc aucun changement dans le sommet 3.
L'arête suivante est (1, 2). Puisque (0 + 4) est supérieur à 2, il n’y aurait pas de mise à jour.
L'arête suivante est (3, 2). Puisque (-6 + 7) est égal à 1, ce qui est inférieur à 3, mettez à jour :
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -6 + 7 = 1
Dans ce cas, la valeur du sommet est mise à jour. Nous concluons donc que l’algorithme de Bellman Ford ne fonctionne pas lorsque le graphique contient le cycle de poids négatif.
Par conséquent, la valeur au sommet 2 est 1.
