FORMULE COTANGENTE

La trigonométrie est une branche importante des mathématiques qui traite de la relation entre les longueurs des côtés et les angles d'un triangle rectangle. Sinus, cosinus, tangente, cosécante, sécante et cotangente sont les six rapports ou fonctions trigonométriques. Où un rapport trigonométrique est représenté comme le rapport entre les côtés d’un triangle rectangle.

sin θ = côté opposé/hypoténuse
cos θ = adjacent side/hypotenuse
tan θ = côté opposé/côté adjacent
cosec θ = 1/sin θ = hypotenuse/opposite side
sec θ = 1/cos θ = hypotenuse/adjacent side
lit bébé θ = 1/tan θ = côté adjacent/côté opposé

Une fonction cotangente est une fonction réciproque de la fonction tangente donnée. La valeur d'un angle cotangent dans un triangle rectangle est le rapport entre la longueur du côté adjacent à l'angle donné et la longueur du côté opposé à l'angle donné. Nous écrivons la fonction cotangente sous la forme cot.

Triangle ABC

Maintenant, la formule cotangente de l'angle θ est :

lit bébé θ = (Côté adjacent)/(Côté opposé)

La fonction cotangente est positive dans les premier et troisième quadrants et négative dans les deuxième et quatrième quadrants.

lit bébé (2π + θ) = lit bébé θ (1^Stquadrant)
lit bébé (π – θ) = – lit bébé θ (2^sdquadrant)
lit bébé (π + θ) = lit bébé θ (3^rdquadrant)
lit bébé (2π – θ) = – lit bébé θ (4^èmequadrant)

La fonction cotangente est une fonction négative puisque la cotangente d'un angle négatif est le négatif d'un angle cotangent positif.

lit bébé (-θ) = – lit bébé θ

En termes de fonction tangente, la fonction cotangente s'écrit :

lit bébé θ = 1/tan θ

(ou)

cot θ = bronzage (90° – θ) (ou) bronzage (π/2 – θ)

La fonction cotangente en termes de fonctions sinus et cosinus peut s'écrire comme suit :

lit bébé θ = cos θ/sin θ

Nous savons que cot θ = côté adjacent/côté opposé

Divisez maintenant le numérateur et le dénominateur par l'hypoténuse

⇒ cot θ = (côté adjacent/hypoténuse) / (côté opposé/hypoténuse)

Nous savons que sin θ = côté opposé/hypoténuse

cos θ = adjacent side/hypotenuse

Par conséquent, cot θ = cos θ/sin θ
installer maven

La fonction cotangente en termes de fonction sinusoïdale peut s'écrire comme suit :

lit bébé θ = (√1 – péché ² i)/péché i

Nous savons que cot θ = cos θ/sin θ

Des identités pythagoriciennes que nous avons ;

parce que²θ + péché²θ = 1

⇒ cos θ = √1 – péché²je

Par conséquent, cot θ = $frac{sqrt{left(1-sin^{2} heta ight)}}{sin heta}$

La fonction cotangente en termes de fonction cosinus peut s'écrire comme suit :

lit bébé θ = cos θ/(√1 -cos ² je)

Nous savons que cot θ = cos θ/sin θ

Des identités pythagoriciennes que nous avons ;

parce que²θ + péché²θ = 1

péché θ = √1 – cos²je

Par conséquent, cot θ = $frac{cos heta}{sqrt{left(1-cos^{2} heta ight)}}$

La fonction cotangente en termes de fonctions sécantes et cosécantes peut s'écrire comme suit :

lit bébé θ = cosec θ/sec θ

Nous avons cot θ = cos θ/sin θ

Cela peut s'écrire sous la forme cot θ = (1/sin θ) / (1/cos θ)

⇒ lit bébé θ = cosec θ/sec θ

La fonction cotangente en termes de fonction cosécante peut s'écrire comme suit :

cot θ = √(cosec ² - 1)

Des identités pythagoriciennes, nous avons,

cosec²θ – lit bébé²θ = 1

⇒ lit bébé²θ = 1 – cosec²- 1

Par conséquent, cot θ = √(cosec²- 1)

La fonction cotangente en termes de fonction sécante peut s'écrire comme suit :

lit bébé θ = 1/(√sec ² je – 1)

Des identités pythagoriciennes, nous avons,

seconde²θ – donc²θ = 1

tan θ = √sec²je – 1

Nous savons que cot θ = 1/tan θ

Ainsi, lit bébé θ = $frac{1}{sqrt{left(1-sec^{2} heta ight)}}$

Tableau des rapports trigonométriques

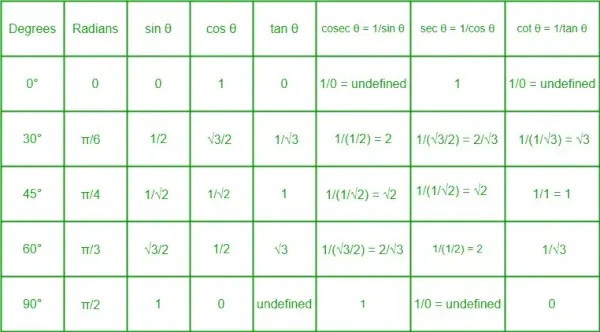
Tableau des rapports trigonométriques

Loi cotangente ou loi des cotangentes

La loi cotangente ressemble à la loi des sinus, mais elle implique ici des demi-angles. La loi des cotangentes décrit la relation entre les longueurs des côtés du triangle et les cotangentes des moitiés des trois angles. Considérons un triangle ABC, où a, b et c sont les longueurs des côtés du triangle.

La loi des cotangentes stipule que,

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

Où s est le demi-périmètre du triangle ABC et r est son rayon intérieur du cercle inscrit du triangle.

s = (une + b + c)/2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

Exemples de problèmes

Problème 1 : Trouver la valeur de cot θ si tan θ = 3/4.

Solution:

Étant donné les données, tan θ = 3/4

Nous savons que, lit bébé θ = 1/tan θ

⇒ lit bébé θ = 1/(3/4) = 4/3

Donc, lit bébé θ = 4/3

Problème 2 : Trouvez la valeur de cot α, sin α = 1/3 et cos α = 2√2/3.

Solution:

Étant donné les données, sin α = 1/3 et cos α = 2√2/3

Nous savons que, cot α = cos α/sin α

⇒ lit bébé α = (2√2/3) / (1/3) = 2√2
java comparer les chaînes

Par conséquent, la valeur de cot α = 2√2

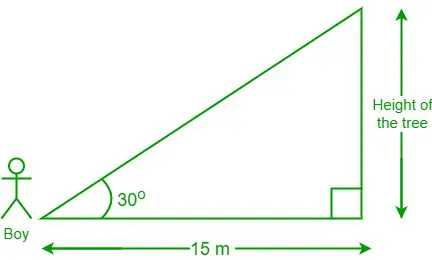
Problème 3 : Un garçon debout à 15 m d’un arbre regarde à un angle de 30 degrés par rapport à la cime de l’arbre. Quelle est la hauteur de l'arbre ?

Solution:

Diagramme à partir des données fournies
conversion de entier en chaîne

Compte tenu des données, la distance entre le garçon et le pied de l'arbre = 15 m et θ = 30°

Soit la hauteur de l'arbre 'h'

Nous avons, lit bébé θ = côté adjacent/côté opposé

⇒ lit bébé 30° = 15/h

⇒ √3 = 15/h [depuis, lit bébé 30° = √3]

⇒ h = 15/√3

⇒ h = 5√3m

Donc la hauteur de l'arbre = 5√3 m

Problème 4 : Trouvez la valeur de cot x si sec x = 6/5.

Solution:

Données données, sec x = 6/5

Nous avons, seconde ² x – donc ² x = 1

⇒ (6/5)²- donc²x = 1

⇒ 36/25 – donc²x = 1

⇒ donc²x = 36/25 – 1

⇒ donc²x = 11/25

⇒ bronzage x = √(11/25) = √11/5

Nous savons que, lit bébé x = 1/tan x

⇒ lit bébé x = 1/(√11/5) = 5/√11

Par conséquent, lit bébé x = 5/√11

Problème 5 : Trouver la valeur de cot θ si cosec θ = 25/24.

Solution:

Données données, cosec θ = 25/24

Nous savons que, cot θ = √(cosec ² - 1)

⇒ lit bébé θ = √(25/24)²- 1

⇒ lit bébé θ =√(625 – 576)/576 = √49/576

⇒ lit bébé θ = 7/24

Par conséquent, la valeur de cot θ = 7/24

Problème 6 : Trouver la valeur de cot β si sin β = 5/13.

Solution:

Étant donné les données, sin β = 5/13
json dans l'exemple json

Nous savons que, sans ² β + cos ² β = 1

⇒ (5/13)²+ parce que²β = 1

⇒ parce que²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ cosβ = √144/169 = 12/13

lit bébé β = cosβ/sin β

= (12/13) / (5/13)

⇒ lit bébé β = 12/5

D’où la valeur de cot β = 12/5

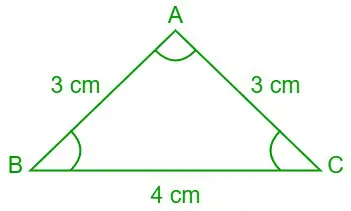
Problème 7 : En utilisant la loi des cotangentes, trouvez les valeurs de ∠A, ∠B et ∠C (en degrés) si les longueurs des trois côtés du triangle ABC sont a = 4 cm, b= 3 cm et c= 3 cm.

Solution:

Étant donné, a = 4 cm, b = 3 cm et c = 3 cm

Triangle ABC

De la loi des cotangentes,

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

s = (une + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

Maintenant, s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

⇒r = √[(1)(2)(2)/5]

Rayon du triangle r = 2/√5

De l'équation de la loi des cotangentes,

lit bébé (A/2)/1 = 1/(2/√5)

⇒ lit bébé (A/2) = √5/2 ⇒ A/2 = lit bébé^-1(√5/2)

⇒ (A/2) = 41,8° ⇒ ∠A = 83,6°

lit bébé(B/2)/2 = 1/(2/√5)

⇒ lit bébé(B/2)/2 = √5/2 ⇒ lit bébé (B/2) = √5

⇒ (B/2) = lit bébé^-1(√5) = 24,1° ⇒ ∠B = 48,2°

lit bébé (C/2)/2 = 1/(2/√5)

⇒ lit bébé(C/2) = √5 ⇒ (C/2) = lit bébé^-1(√5)

⇒ (C/2) = 24,1° ⇒ ∠C = 48,2°

Ainsi, les angles du triangle ABC sont ∠A = 83,6°, ∠B = 48,2° et ∠C = 48,2°.