Système de numération binaire est un système numérique utilisé pour représenter divers nombres en utilisant seulement deux symboles 0 et 1. Le mot binaire est dérivé du mot bi qui signifie deux. Par conséquent, ce système de numérotation est appelé système de numérotation binaire. Ainsi, le système de nombres binaires est un système qui ne comporte que deux symboles.
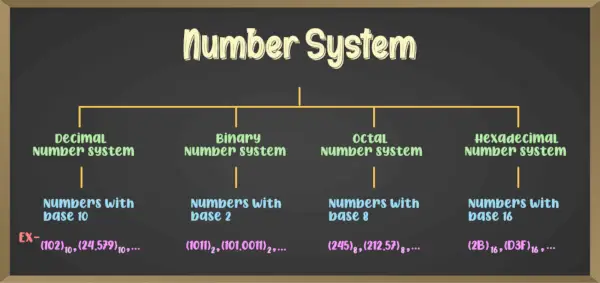
Il existe généralement différents types de systèmes numériques et parmi eux, les quatre principaux sont :
- Système de numérotation binaire (système de numérotation avec base 2)
- Système de numérotation octale (système de numérotation avec base 8)
- Système de nombres décimaux (système de nombres avec base 10)
- Système de nombres hexadécimaux (système de nombres avec base 16)
Ici, nous allons seulement en apprendre davantage sur le système de nombres binaires. Ce système numérique est très utile pour expliquer les tâches à l'ordinateur. Dans le système de nombres binaires, nous avons deux états 0 et 1 et ces deux états sont représentés par deux états d'un transistor. Si le courant traverse le transistor, l'ordinateur lit 1 et si le courant est absent du transistor, il lit 0. Ainsi, en alternant le courant, l'ordinateur lit le système de nombres binaires. Chaque chiffre du système de numérotation binaire est appelé un bit.
Dans cet article, nous découvrirons en détail le système de nombres binaires, la conversion du système de nombres binaires, la table binaire, le fonctionnement des nombres binaires, des exemples et d'autres.
Table des matières
- Système de numération binaire
- Tableau des nombres binaires
- Conversion binaire en décimal
- Conversion décimale en binaire
- Opérations arithmétiques sur les nombres binaires
- Complément de 1 et 2 d'un nombre binaire
- Utilisations du système de nombres binaires
- Exemple de système de nombres binaires
Système de numération binaire
Le système numérique binaire est le système numérique dans lequel nous utilisons deux chiffres 0 et 1 pour effectuer toutes les opérations nécessaires. Dans le système de nombres binaires, nous avons une base de 2. La base du système de nombres binaires est également appelée base du système de numérotation .
Dans un système de nombres binaires, nous représentons le nombre comme suit :
- (11001)2
Dans l'exemple ci-dessus, un nombre binaire est donné dont la base est 2. Dans un système de nombres binaires, chaque chiffre est appelé le bit. Dans l'exemple ci-dessus, il y a 5 chiffres.
Tableau des nombres binaires
| Nombre décimal | Nombre binaire | Nombre décimal | Nombre binaire |
|---|---|---|---|
| 1 | 001 | onze | 1011 |
| 2 | 010 | 12 | 1100 |
| 3 | 011 | 13 | 1101 |
| 4 | 100 | 14 | 1110 |
| 5 | 101 | quinze | 1111 |
| 6 | 110 | 16 | 10000 |
| 7 | 111 | 17 | 10001 |
| 8 | 1000 | 18 | 10010 |
| 9 | 1001 | 19 | 10011 |
| dix | 1010 | vingt | 10100 |
Conversion binaire en décimal
Un nombre binaire est converti en nombre décimal en multipliant chaque chiffre du nombre binaire par la puissance 1 ou 0 à la puissance correspondante de 2. Considérons qu'un nombre binaire a n chiffres, B = an-1…un3un2un1un0. Maintenant, le nombre décimal correspondant est donné par
D = (un n-1 ×2 n-1 ) +…+(une 3 ×2 3 ) + (un 2 ×2 2 ) + (un 1 ×2 1 ) + (un 0 ×2 0 )
Passons en revue un exemple pour mieux comprendre le concept.
Exemple : Convertir (10011) 2 à un nombre décimal.
Solution:
Le nombre binaire donné est (10011)2.
(10011)2= (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (1 × 20)
= 16 + 0 + 0 + 2 + 1 = (19)dix
D'où le nombre binaire (10011)2s'exprime par (19)dix.
Conversion décimale en binaire
Un nombre décimal est converti en nombre binaire en divisant le nombre décimal donné par 2 de manière continue jusqu'à ce que nous obtenions le quotient de 1, et nous écrivons les nombres de bas en haut.
Passons en revue un exemple pour mieux comprendre le concept.
Exemple : Convertir (28) dix en un nombre binaire.
Solution:
Par conséquent, (28)dixest exprimé par (11100)2.
Opérations arithmétiques sur les nombres binaires
Nous pouvons facilement effectuer diverses opérations sur les nombres binaires. Diverses opérations arithmétiques sur le nombre binaire comprennent :
- Addition binaire
- Soustraction binaire
- Multiplication binaire
- Division binaire
Apprenons maintenant la même chose en détail.
Addition binaire
Le résultat de l’addition de deux nombres binaires est également un nombre binaire. Pour obtenir le résultat de l’addition de deux nombres binaires, il faut additionner chiffre des nombres binaires par chiffre. Le tableau ajouté ci-dessous montre la règle d'addition binaire.
| Nombre binaire (1) | Nombre binaire (2) | Ajout | Porter |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 mot-clé volatile java | 0 |
| 1 | 1 | 0 | 1 |
Soustraction binaire
Le résultat de la soustraction de deux nombres binaires est également un nombre binaire. Pour obtenir le résultat de la soustraction de deux nombres binaires, il faut soustraire chiffre des nombres binaires par chiffre. Le tableau ajouté ci-dessous montre la règle de soustraction binaire.
| Nombre binaire (1) | Nombre binaire (2) | Soustraction | Emprunter |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Multiplication binaire
Le processus de multiplication des nombres binaires est similaire à la multiplication des nombres décimaux. Les règles pour multiplier deux nombres binaires sont données dans le tableau,
| Nombre binaire (1) | Nombre binaire (2) | Multiplication |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Division binaire
Le méthode de division pour les nombres binaires est similaire à celle de la méthode de division des nombres décimaux. Passons en revue un exemple pour mieux comprendre le concept.
Exemple : Diviser (101101) 2 par (110) 2
Solution:
Complément de 1 et 2 d'un nombre binaire
- Le complément de 1 d'un nombre binaire est obtenu en inversant les chiffres du nombre binaire.
Exemple : Trouver le complément à 1 de (10011) 2 .
Solution:
Le nombre binaire donné est (10011)2
Maintenant, pour trouver son complément à 1, il faut inverser les chiffres du nombre donné.
Ainsi, le complément à 1 de (10011)2est (01100)2
- Le complément à 2 d'un nombre binaire est obtenu en inversant les chiffres du nombre binaire puis en ajoutant 1 au bit le moins significatif.
Exemple : Trouver le complément à 2 de (1011) 2 .
Solution:
Le nombre binaire donné est (1011)2
Pour trouver le complément à 2, trouvez d’abord son complément à 1, c’est-à-dire (0100)2
Maintenant, en ajoutant 1 au bit le moins significatif, on obtient (0101)2
D’où le complément à 2 de (1011)2est (0101)2
Utilisations du système de nombres binaires
Les systèmes de nombres binaires sont utilisés à diverses fins et l'utilisation la plus importante du système de nombres binaires est,
aligner l'image CSS
- Le système de nombres binaires est utilisé dans tous les appareils électroniques numériques pour effectuer diverses opérations.
- Les langages de programmation utilisent le système de nombres binaires pour coder et décoder les données.
- Le système de nombres binaires est utilisé dans les sciences des données à diverses fins, etc.
En savoir plus,
- Formule binaire
- Différence entre les systèmes de nombres décimaux et binaires
Exemple de système de nombres binaires
Exemple 1 : Convertir un nombre décimal (98) dix en binaire.
Solution:
Ainsi, le nombre binaire pour (98)dixest égal à (1100010)2
Exemple 2 : Convertir un nombre binaire (1010101) 2 en nombre décimal.
Solution:
Nombre binaire donné, (1010101)2
= (1 × 20) + (0 × 21) + (1 × 22) + (0 × 23) + (1 × 24) + (0 × 25) + (1×26)
= 1 + 0 + 4 + 0 + 16 + 0 + 64
= (85)dix
Ainsi, le nombre binaire (1010101)2est égal à (85)dixen système décimal.
Exemple 3 : Diviser (11110) 2 par (101) 2
Solution:
Exemple 4 : Ajouter (11011) 2 et (10100) 2
Solution:
Par conséquent, (11011)2+ (10100)2= (101111)2
Exemple 5 : Soustraire (11010) 2 et (10110) 2
Solution:
Par conséquent, (11010)2– (10110)2= (00100)2
Exemple 6 : Multiplier (1110) 2 et (1001) 2 .
Solution:
Ainsi, (1110)2× (1001)2= (1111110)2
FAQ sur le système de nombres binaires
Qu'est-ce qu'un système de nombres binaires ?
Le système de numérotation binaire est l'un des quatre systèmes de numérotation utilisés pour représenter les nombres en utilisant seulement deux chiffres, 0 et 1. Dans le système de numérotation binaire, les chiffres sont appelés « bits ». Le système de nombres binaires est utilisé par les ordinateurs pour effectuer divers calculs.
Qu'est-ce qu'un B il?
Un bit dans le système de numérotation binaire est défini comme un chiffre individuel contenant la valeur « 0 » ou « 1 ».
Qu'est-ce qu'un grignotage ?
Un groupe de quatre chiffres s'appelle la Niblle.
Quelle est la valeur binaire de 10 ?
La valeur binaire de 10 est (1010)2
Quels sont les types de systèmes numériques ?
Il existe différents types de systèmes numériques et certains d'entre eux sont,
- Système de numération binaire
- Système de numérotation octale
- Système de nombres décimaux
- Système de nombres hexadécimaux
Comment calculer des nombres binaires ?
Les nombres binaires sont calculés à partir de nombres décimaux en divisant le nombre décimal par 2 et en écrivant le reste. Ensuite, nous classons tous les restes du plus récent au plus ancien pour obtenir le nombre binaire.
Comment ajouter des nombres binaires ?
Les nombres binaires sont ajoutés en utilisant les formules écrites ci-dessous,
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (porter 1)






