Un arbre binaire est équilibré si la hauteur de l'arbre est O (Log n) où n est le nombre de nœuds. Par exemple, l'arbre AVL maintient la hauteur O (Log n) en s'assurant que la différence entre les hauteurs des sous-arbres gauche et droit est d'au plus 1. Les arbres rouge-noir maintiennent la hauteur O (Log n) en s'assurant que le nombre Le nombre de nœuds noirs sur chaque chemin racine-feuille est le même et il n'y a pas de nœuds rouges adjacents. Les arbres de recherche binaire équilibrée sont bons en termes de performances car ils fournissent un temps O (log n) pour la recherche, l'insertion et la suppression.
variable de référence en Java
Un arbre binaire équilibré est un arbre binaire qui respecte les 3 conditions :
- La hauteur des arbres gauche et droit pour chaque nœud ne diffère pas de plus de 1.
- Le sous-arbre gauche de ce nœud est également équilibré.
- Le sous-arbre droit de ce nœud est également équilibré.
Un seul nœud est toujours équilibré. Il est également appelé arbre binaire équilibré en hauteur.
Exemple :
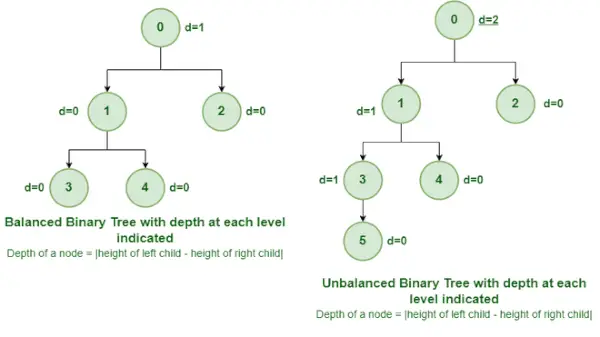
Arbre binaire équilibré et déséquilibré
C'est un type d'arbre binaire dans lequel la différence entre la hauteur du sous-arbre gauche et droit pour chaque nœud est soit 0, soit 1. Dans la figure ci-dessus, le nœud racine ayant une valeur 0 est déséquilibré avec une profondeur de 2 unités. .
Application de l'arbre binaire équilibré :
- Arbres AVL
- Arbre Noir Rouge
- Arbre de recherche binaire équilibré
Avantages de l’arbre binaire équilibré :
- Les mises à jour non destructives sont prises en charge par un arbre binaire équilibré avec la même efficacité asymptotique.
- Les requêtes de plage et les itérations dans le bon ordre sont rendues possibles par l'arbre binaire équilibré.
