La vitesse est simplement la mesure de la vitesse à laquelle un objet se déplace, comme la vitesse à laquelle vous conduisez une voiture. Or, nous parlons ici d’un type spécifique de vitesse. La vitesse angulaire est uniquement un type de vitesse, mais ici, le corps doit se déplacer selon une trajectoire circulaire.
Formule de vitesse angulaire
La vitesse angulaire est définie comme le taux de variation du déplacement angulaire, c'est-à-dire l'angle parcouru par un corps le long d'une trajectoire circulaire. La vitesse angulaire est calculée en termes de nombre de rotations/révolutions effectuées par un corps par rapport au temps pris. La vitesse angulaire est désignée par la lettre grecque « ω » connue sous le nom d'Omega. L'unité SI de vitesse angulaire est le rad/s.
La vitesse angulaire est calculée à l'aide de deux formules différentes,
- ω = θ/t ω = v/r
Dérivation de formule
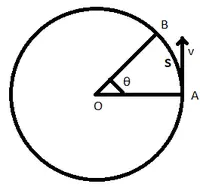
Considérons un corps se déplaçant sur une trajectoire circulaire de rayon r indiqué ci-dessus avec une vitesse linéaire v. Supposons que le corps se déplace du point A au point B parcourant une distance s à travers l'arc de cercle et parcourant un angle θ dans la période de temps t.
Chemin circulaire couvert par un corps
Comme on le sait, la vitesse angulaire est le taux de changement de déplacement – Vitesse angulaire, ω = θ/t
La formule de la vitesse angulaire est donc ω = θ/t .
Une autre formule pour la vitesse angulaire
Malgré la formule indiquée ci-dessus, il existe une autre formule, plus largement utilisée, pour calculer la vitesse angulaire du point de vue des concours.
Comme ω = θ/t ⇢ (1)
Nous savons maintenant que la distance parcourue sur un arc de cercle est égale au rayon multiplié par l'angle parcouru. Donc,
s = rθ
=> θ = s/r ⇢ (2)
désactiver le mode développeur AndroidDe (1) et (2),
ω = s/(rt) ⇢ (3)
Également à partir d'une compréhension générale des vitesses linéaires,
v = s/t ⇢ (4)
De (3) et (4),
ω = v/r
Exemples de problèmes
Question 1 : Considérons un corps se déplaçant le long d’une trajectoire circulaire de rayon 5 m. Il couvre une demi-révolution en 5s. Calculez sa vitesse angulaire.
Solution:
En demi-tour, l'angle parcouru est de 180 degrés. En radians, il est égal à π radians.
ω = θ/t
=> ω = π/5 = 0,628 rad/s
Question 2 : Une roue de voiture d'un rayon de 2 m tourne avec une vitesse linéaire de 10 m/s. Calculez sa vitesse angulaire.
Solution:
ω = v/r
ω = 10/2
= 5 rad/s
Question 3 : Considérons une voiture de course circulant sur une piste circulaire avec une vitesse de 18 km/h et le rayon de la piste est de 0,2 m. Calculez la vitesse angulaire de la voiture.
Solution:
v = 18 km/h = 5 m/s
r = 0,2 m
ω = v/r
= 5/0,2
= 25 rads/s
Question 4 : Une voiture se déplace le long d'une trajectoire circulaire d'un rayon de 2 m avec une vitesse angulaire de 2 rad/s. Calculez l'angle en degrés par lequel la voiture se déplace en 2 secondes.
Solution:
Donné, ω = 2 rad/s et t = 2s
Puisque ω = θ/t => θ = ωt
=> θ = (2 × 2) = 4 rads
En degrés, θ = 4 × (180/π) = 229,18 degrés
Question 5 : Combien de tours un corps a-t-il effectué en se déplaçant le long d'une trajectoire circulaire avec une vitesse angulaire de 7π rad/s en 0,5 s ?
Solution:
Étant donné ω = 7π rad/s et t = 0,5s
Puisque ω = θ/t => θ = ωt
θ = (7π × 0,5) = 3,5π
En 2π rad, les révolutions parcourues sont de 1
=> En 1 rad, la révolution parcourue est de (1/2π)
=> En 3,5π rad, tours = 3,5π/2π = 1,75 tours
Ainsi, le corps effectuera 1 tour complet et 3/4 du prochain tour en 0,5 s.
Question 6 : Quelle sera la vitesse angulaire d'un corps se déplaçant sur une trajectoire circulaire de rayon 2m qui couvre 4m d'arc de longueur 5s.
Solution:
Étant donné s = 4m, r = 2m, t = 5s
En utilisant la formule s = rθ => θ = s/r
θ = 4/2 = 2 rads
Puisque ω = θ/t
caractère dans la chaîne=> ω = 2/5 = 0,4 rad/s