L'angle entre deux vecteurs est l'angle entre leurs queues et cet angle peut être facilement trouvé à l'aide du produit vectoriel et du produit scalaire des formules vectorielles. L'angle entre deux vecteurs est toujours compris entre 0° et 180°.
Dans cet article, nous apprendrons en détail l'angle entre deux vecteurs, la définition, les formules et les exemples.
Qu'est-ce que l'angle entre deux vecteurs ?
L'angle entre deux vecteurs est l'angle formé à l'intersection de leurs queues. L'angle entre deux vecteurs peut être aigu, droit ou obtus, selon la direction des vecteurs.
L'angle entre deux vecteurs est trouvé à l'aide de deux formules :
- Utilisation du produit scalaire de vecteurs
- Utilisation du produit croisé de vecteurs
Ceci est expliqué dans la formule ci-dessous.
Angle entre deux formules vectorielles
Angle entre deux vecteurs se trouve facilement et le plus souvent en utilisant le produit scalaire de vecteurs.

Deux vecteurs A et B
Produit scalaire de A et B est donné par,
vec{A}.vec{B} = |UNE| |B| cosθ.
Cas spéciaux
- Lorsque l'angle entre les vecteurs est de 0 degré.
Soit θ = 0°
⇒ |UNE| |B| cosθ
⇒ |A| |B| cos0°
⇒ |A| |B| [cos0° = 1]
- Lorsque l'angle entre les vecteurs est de 180 degrés.
⇒ |UNE| |B| cosθ
⇒ |UNE| |B| cos180°
⇒ – |UNE| |B| [cos180° = -1]
- Lorsque l'angle entre les vecteurs est de 90 degrés.
⇒ |UNE| |B| cosθ
⇒ |UNE| |B| cos90°
⇒ |UNE| |B| × 0 [cos90° = 0]
⇒ 0
Formule pour l'angle entre deux vecteurs
Le cosinus de l'angle entre deux vecteurs est égal à la somme du produit des constituants individuels des deux vecteurs, divisée par le produit de la grandeur des deux vecteurs.
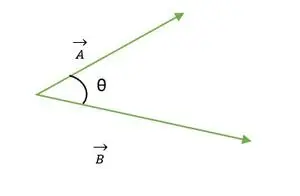
Deux vecteurs A et B
cosθ=
θ= cos-1
Sous forme cartésienne,
UNE = UNEXje + Aetj + AAveck
B = BXje + Betj + BAveck
cos θ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}
Propriétés du produit Dot
- Le produit scalaire est commutatif
vec{A}.vec{B}=vec{B}.vec{A}
- Le produit scalaire est distributif
vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})
L'angle entre deux vecteurs est compris entre 0 ≤ θ ≤ 180. Lorsque les queues ou les têtes des deux vecteurs coïncident, l'angle entre les vecteurs est calculé.
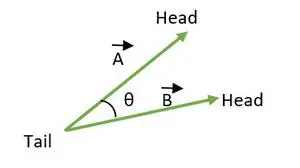
Queue coïncide
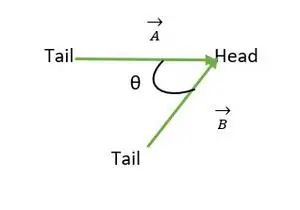
Coïncidence de la tête
Exemples de problèmes Angle entre deux vecteurs Formule
Problème 1 : Trouver l'angle entre les vecteurs (s'ils forment un triangle équilatéral)
- vecteurs a et b
- vecteurs b et c
- vecteurs a et c
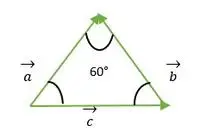
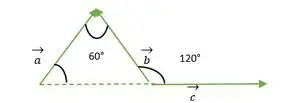
Triangle équilatéral formé par les vecteurs a, b, c
Solution:
- vecteurs a et b
Pour les vecteurs a et b, les têtes des deux vecteurs coïncident l'une avec l'autre, donc l'angle entre les vecteurs a et b est le même que l'angle entre deux côtés du triangle équilatéral = 60°.
- vecteurs b et c :
D’après la figure ci-dessus, nous voyons que la tête ou la queue des vecteurs b et c ne coïncident pas.
Ainsi, en utilisant la propriété : Un vecteur reste inchangé s'il est transmis parallèlement à lui-même.
Le vecteur c est décalé parallèlement à lui-même
Nous voyons maintenant que les queues des vecteurs b et c coïncident l'une avec l'autre, c'est donc la même chose que l'angle extérieur fait avec un triangle équilatéral = 120°.
- vecteurs a et c
Les queues de a et c coïncident
Pour les vecteurs a et c, les queues des deux vecteurs coïncident, donc l'angle entre les vecteurs a et c est le même que l'angle entre deux côtés du triangle équilatéral = 60°.
Problème 2 : Trouver les angles entre les vecteurs s’ils forment un triangle rectangle isocèle.
- vecteur a et b
- vecteur b et c
- vecteurs a et c
Solution:
- vecteur a et b
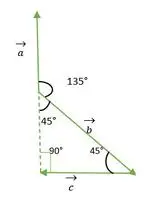
Triangle isocèle à angle droit
D’après la figure ci-dessus, nous voyons que la tête ou la queue des vecteurs a et b ne coïncident pas. Ainsi, en utilisant la propriété : Un vecteur reste inchangé s'il est transmis parallèlement à lui-même.
un vecteur est décalé parallèlement à lui-même
Maintenant, les queues des vecteurs a et b coïncident l’une avec l’autre et forment un angle identique à l’angle extérieur d’un triangle isocèle à angle droit = 135°.
- vecteur b et c
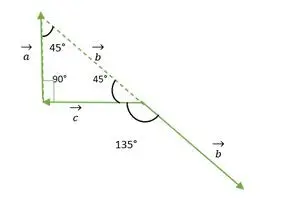
Triangle isocèle à angle droit
D'après la figure ci-dessus, les vecteurs tête ou queue b et c ne coïncident pas. Ainsi, en utilisant la propriété, un vecteur reste inchangé s’il est transmis parallèlement à lui-même.
le vecteur b est décalé parallèlement à lui-même
Maintenant, les queues des vecteurs b et c coïncident l’une avec l’autre et forment un angle identique à l’angle extérieur d’un triangle isocèle à angle droit = 135°.
- vecteurs a et c
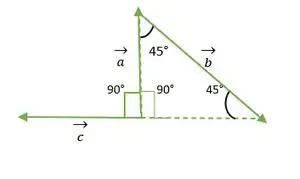
Triangle isocèle à angle droit
D'après la figure ci-dessus, les têtes ou queues des vecteurs a et c ne coïncident pas. Ainsi, en utilisant la propriété : Un vecteur reste inchangé s'il est transmis parallèlement à lui-même.
c le vecteur est déplacé parallèlement à lui-même
Maintenant, les queues des vecteurs a et c coïncident l’une avec l’autre et forment un angle identique à l’angle droit du triangle isocèle = 90°.
Problème 3 : Trouver l'angle entre les vecteurs A = i + j + k et le vecteur B = -2i – 2j – 2k.
Solution:
De la formule,
UNE = UNEXje + Aetj + AAveck
B = BXje + Betj + BAveck
cosθ=
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Ici, dans la question donnée,
A = je + j + k
B = -2i -2j -2k
Remplacement des valeurs dans la formule
⇒ cosθ =
frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})} ⇒ cosθ =
frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})} ⇒ cosθ =
frac{-6}{(sqrt{3}×sqrt{12})} ⇒ cosθ =
frac{-6}{(sqrt{36})} ⇒ cosθ = -6/6
⇒ cosθ= -1
⇒ θ = 180°
Problème 4 : Trouver l'angle entre le vecteur A = 3i + 4j et B = 2i + j
Solution:
UNE = UNEXje + Aetj + AAveck
B = BXje + Betj + BAveck
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Ici étant donné,
UNE= 3i + 4j + 0k
B = 2i + j + 0k
En remplaçant les valeurs dans la formule,
⇒ cosθ =
frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})} ⇒ cosθ =
frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})} ⇒ cosθ =
frac{(10)}{(sqrt{25}×sqrt{5})} ⇒ cosθ =
frac{(10)}{(sqrt{125})} ⇒ θ = cos-1(
frac{(10)}{5.(sqrt{5})} )⇒ θ = cos-1(
frac{2}{(sqrt{5})} )
Problème 5 : Trouvez l'angle entre le vecteur A = i + j et le vecteur B = j + k.
Solution:
De la formule,
UNE = UNEXje + Aetj + AAveck
B = BXje + Betj + BAveck
combien de villes y a-t-il aux États-Uniscosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Ici, dans la question donnée,
⇒ UNE = je + j
⇒ B = j + k
⇒ cosθ =
frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})} ⇒ cosθ =
frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})} ⇒ cosθ =
frac{1}{(sqrt{2}×sqrt{2})} ⇒ θ = cos-1(1/2)
⇒ θ = 60°