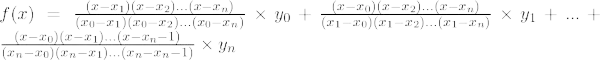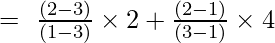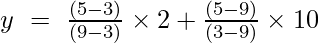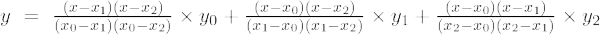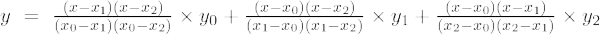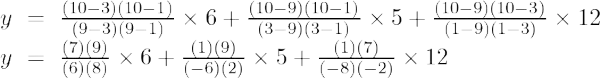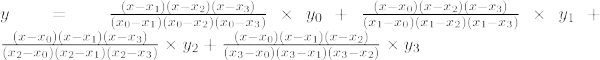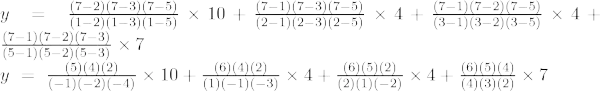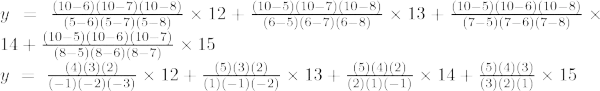FORMULE D'INTERPOLATION DE LAGRANGE : PREUVE, EXEMPLES ET FAQ

Formule d'interpolation de Lagrange trouve un polynôme appelé Polynôme de Lagrange qui prend certaines valeurs en un point arbitraire. C'est un nième degréexpression polynomiale de la fonction f(x). La méthode d'interpolation est utilisée pour trouver les nouveaux points de données dans la plage d'un ensemble discret de points de données connus.

noeud de liste Java

Dans cet article, nous découvrirons l'interpolation de Lagrange, la formule d'interpolation de Lagrange, la preuve de la formule d'interpolation de Lagrange, les exemples basés sur la formule d'interpolation de Lagrange et d'autres en détail.

Qu’est-ce que l’interpolation de Lagrange ?

L'interpolation de Lagrange est un moyen de trouver la valeur d'une fonction à un moment donné lorsque la fonction n'est pas donnée. Nous utilisons d'autres points de la fonction pour obtenir la valeur de la fonction à tout point requis.

Supposons que nous ayons une fonction y = f(x) dans laquelle la substitution des valeurs de x donne différentes valeurs de y. Et on nous donne deux points (x₁, et₁) et (x₂, et₂) sur la courbe, la valeur de y à x = a(constante) est calculée à l'aide de la formule d'interpolation de Lagrange.

Formule d'interpolation de Lagrange

Étant donné peu de valeurs réelles x₁, X₂, X₃, …, X_nAndy₁, et₂, et₃, …, et_net il y aura un polynôme P à coefficients réels satisfaisant les conditions P(x_je) = et_je, ∀ i = {1, 2, 3, …, n} et le degré du polynôme P doit être inférieur au nombre de valeurs réelles, c'est-à-dire le degré (P)

Formule d'interpolation de Lagrange pour le nième ordre

La formule d'interpolation de Lagrange pour n^èmeLe polynôme de degré est donné ci-dessous :

Formule d'interpolation de Lagrange pour le n ^ème l'ordre est,

$f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} imes y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n$

Formule d'interpolation du premier ordre de Lagrange

Si laLe degré du polynôme est 1, on l'appelle alors polynôme du premier ordre. Formule d'interpolation de Lagrange pour 1^Stles polynômes d'ordre sont,

$f(x)~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1$

Formule d'interpolation de Lagrange du second ordre

Si le degré du polynôme est 2, alors il est appelé polynôme du second ordre. La formule d'interpolation de Lagrange pour les polynômes du 2ème ordre est,

$f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2$

Preuve du théorème de Lagrange

Considérons un polynôme du nième degré de la forme donnée,

f(x) = UNE₀(x – x₁)(x – x₂)(x – x₃)…(x – x_n) + UNE₁(x – x₁)(x – x₂)(x – x₃)…(x – x_n) + … + A_(n-1)(x – x₁)(x – x₂)(x – x₃)…(x – x_n)

Observations de remplacement x_jepour obtenir un_je

Mettez x = x₀alors nous obtenons A₀

f(x₀) = et₀= Un₀(X₀- X₁)(X₀- X₂)(X₀- X₃)…(X₀- X_n)

UN ₀ = et ₀ /(X ₀ - X ₁ )(X ₀ - X ₂ )(X ₀ - X ₃ )…(X ₀ - X _n )

En remplaçant x = x₁nous obtenons un₁

f(x₁) = et₁= Un₁(X₁- X₀)(X₁- X₂)(X₁- X₃)…(X₁- X_n)

UN ₁ = et ₁ /(X ₁ - X ₀ )(X ₁ - X ₂ )(X ₁ - X ₃ )…(X ₁ - X _n )

De même, en substituant x = x_nnous obtenons un_n

f(x_n) = et_n= Un_n(X_n- X₀)(X_n- X₁)(X_n- X₂)…(X_n- X_n-1)

UN _n = et _n /(X _n - X ₀ )(X _n - X ₁ )(X _n - X ₂ )…(X _n - X _n-1 )

Si nous substituons toutes les valeurs de A_jeen fonction f(x) où i = 1, 2, 3,…n alors nous obtenons la formule d'interpolation de Lagrange comme,

$f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} fois y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)}fois y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n$

Propriétés de la formule d'interpolation de Lagrange

Diverses propriétés de la formule d'interpolation de Lagrange sont discutées ci-dessous,

Cette formule est utilisée pour trouver la valeur de la fonction à tout moment même lorsque la fonction elle-même n'est pas donnée.
Il est utilisé même si les points donnés ne sont pas régulièrement espacés.
Il donne la valeur de la variable dépendante pour toute variable indépendante appartenant à n'importe quelle fonction et est donc utilisé en analyse numérique pour trouver les valeurs de la fonction, etc.

Utilisations de la formule d'interpolation de Lagrange

Diverses utilisations de la formule d'interpolation de Lagrange sont discutées ci-dessous,

Il est utilisé pour trouver la valeur de la variable dépendante pour une variable indépendante particulière, même si la fonction elle-même n'est pas donnée.
Il est utilisé dans la mise à l'échelle des images.
Il est utilisé dans la modélisation de l'IA.
Il est utilisé pour enseigner la PNL, etc.

En savoir plus,

Formule d'interpolation
Formule d'interpolation linéaire

Exemples utilisant la formule d'interpolation de Lagrange

Examinons quelques exemples de questions sur la formule d'interpolation de Lagrange.

Exemple 1 : Trouver la valeur de y à x = 2 pour l'ensemble de points donné (1, 2), (3, 4)

Solution:

Donné,

(X₀, et₀) = (1, 2)
(X₁, et₁) = (3, 4)
La formule d'interpolation de Lagrange du premier ordre est,

$y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1$

À x = 2

et $=~frac{(2-3)}{(1-3)} imes 2+frac{(2-1)}{(3-1)} imes 4$

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

La valeur de y à x = 2 est 3

Exemple 2 : Trouver la valeur de y à x = 5 pour l'ensemble de points donné (9, 2), (3, 10)

Solution:

Donné,

(X₀, et₀) = (9, 2)
(X₁, et₁) = (3, 10)
La formule d'interpolation de Lagrange du premier ordre est,

$y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1$

À x = 5

$y~=~frac{(5-3)}{(9-3)} imes 2+frac{(5-9)}{(3-9)} imes 10$

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7,33

La valeur de y à x = 5 est 7,33

Exemple 3 : Trouver la valeur de y à x = 1 pour l'ensemble de points donné (1, 6), (3, 4), (2, 5)

Solution:

ajouter la gestion des exceptions Java

Donné,

(X₀, et₀) = (1, 6)
(X₁, et₁) = (3, 4)
(X₂, et₂) = (2, 5)
La formule d'interpolation de Lagrange du deuxième ordre est,

$y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2$

À x = 1

$y~=~frac{(1-3)(1-2)}{(1-3)(1-2)} imes 6+frac{(1-1)(1-2)}{( 3-1)(3-2)}fois 4+frac{(1-1)(1-3)}{(2-1)(2-3)}fois 5 y~=~ frac{(-2)(-1)}{(-2)(-1)} imes 6+frac{(0)(-1)}{(2)(1)} imes 4+frac {(0)(-2)}{(1)(-1)}fois 5$

y = (12/2) + 0 + 0

y = 6

La valeur de y à x = 1 est 6

Exemple 4 : Trouver la valeur de y à x = 10 pour l'ensemble de points donné (9, 6), (3, 5), (1, 12)

Solution:

Donné,

(X₀, et₀) = (9, 6)
(X₁, et₁) = (3, 5)
(X₂, et₂) = (1, 12)
La formule d'interpolation de Lagrange du deuxième ordre est,

$y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2$

À x = 10

$y~=~frac{(10-3)(10-1)}{(9-3)(9-1)} imes 6+frac{(10-9)(10-1)}{( 3-9)(3-1)} imes 5+frac{(10-9)(10-3)}{(1-9)(1-3)} imes 12 y~=~ frac{(7)(9)}{(6)(8)} imes 6+frac{(1)(9)}{(-6)(2)} imes 5+frac{(1) (7)}{(-8)(-2)}fois 12$
tranche java

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9,375

La valeur de y à x = 10 est 9,375

Exemple 5 : Trouver la valeur de y à x = 7 pour l'ensemble de points donné (1, 10), (2, 4), (3, 4), (5, 7)

Solution:

Donné,

(X₀, et₀) = (1, 10)
(X₁, et₁) = (2, 4)
(X₂, et₂) = (3, 4)
(X₃, et₃) = (5, 7)
La formule d'interpolation de Lagrange du troisième ordre est,

$y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)}fois y_3$

À x = 7

$y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)} imes 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)} imes 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)} imes 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)}fois 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)}fois 10+ frac{(6)(4)(2)}{(1)(-1)(-3)} imes 4+frac{(6)(5)(2)}{(2)(1) (-2)}fois 4+frac{(6)(5)(4)}{(4)(3)(2)}fois 7$

y = -50 + 64 – 60 + 35

y = 99 – 110 = -onze

La valeur de y à x = 7 est -11

Exemple 6 : Trouver la valeur de y à x = 10 pour l'ensemble de points donné (5, 12), (6, 13), (7, 14), (8, 15)

Solution:

Donné,
java faire une boucle while

(X₀, et₀) = (5, 12)
(X₁, et₁) = (6, 13)
(X₂, et₂) = (7, 14)
(X₃, et₃) = (8, 15)
La formule d'interpolation de Lagrange du troisième ordre est,

$y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)}fois y_3$

À x = 10,

$y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)} imes 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)} imes 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)} imes 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)}fois 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)}fois 12+ frac{(5)(3)(2)}{(1)(-1)(-2)} imes 13+frac{(5)(4)(2)}{(2)(1) (-1)}fois 14+frac{(5)(4)(3)}{(3)(2)(1)}fois 15$

y = -48 + 195 – 280 + 150

y = 17

La valeur de y à x = 10 est 17

Exemple 7 : Trouver la valeur de y à x = 0 pour l'ensemble de points donné (-2, 5), (1, 7)

Solution:

Donné,

(X₀, et₀) = (-2, 5)
(X₁, et₁) = (1, 7)
La formule d'interpolation de Lagrange du premier ordre est,

$y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1$

À x = 0,

$y~=~frac{(0-1)}{(-2-1)} imes 5+frac{(0+2)}{(1+2)} imes 7$

y = (5/3) + (14/3)

y = 19/3 = 6,33

La valeur de y à x = 0 est 6,33

FAQ sur la formule d'interpolation de Lagrange

1. Qu'est-ce que la formule d'interpolation de Lagrange ?

La formule d'interpolation de Lagrange est une formule utilisée pour trouver la valeur de la variable dépendante de la fonction pour toute variable indépendante même si la fonction elle-même n'est pas donnée.

2. Quelles sont les applications de la formule d’interpolation de Lagrange ?

La formule de Lagranges a diverses applications dans les mathématiques modernes et les sciences des données,

Il est utilisé pour modéliser l'IA Traning.
Il est utilisé dans le traitement d'images.
Il est utilisé dans le graphisme de courbes 3D et supérieures, etc.

3. Qu'est-ce que la formule d'interpolation de Lagrange du premier ordre ?

La formule d'interpolation de Lagranges du premier ordre est :

f(x) = (x – x ₁ )/(X ₀ - X ₁ )×f ₀ + (x – x ₀ )/(X ₁ - X ₀ )×f ₁

4. Qu'est-ce que la formule d'interpolation de Lagrange du second ordre ?

La formule d'interpolation de Lagranges du deuxième ordre est la suivante :

f(x) = [(x – x ₁ )(x – x ₂ )/(X ₀ - X ₁ )(X ₀ - X ₂ )]×f ₀ + [(x – x ₀ )(x – x ₂ )/(X ₁ - X ₀ )(X ₁ - X ₂ )]×f ₁ + [(x – x ₀ )(x – x ₁ )/(X ₂ - X ₀ )(X ₂ - X ₂ )]×f ₀